この世の中の物質は、たった数グラムの物質でもおおよそ1023個の、膨大な数の原子・分子から成り立っており、これらの原子・分子は相互作用を通して、互いに複雑な影響を及ぼしあっています。
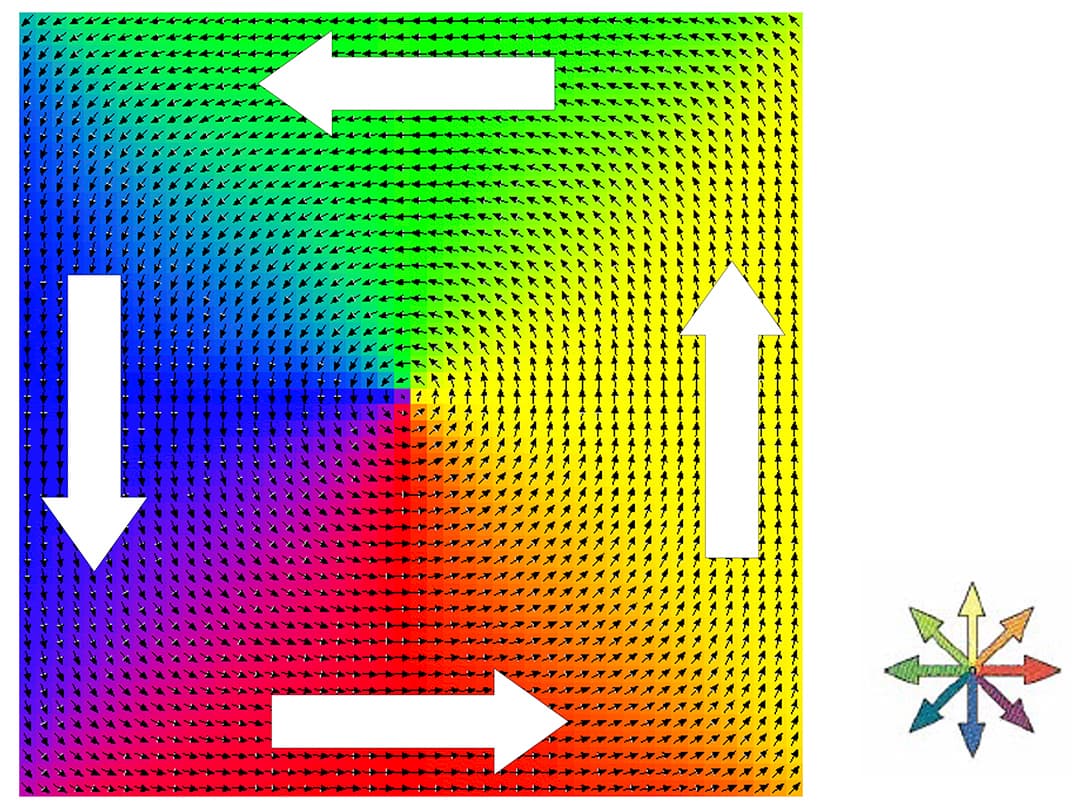
その結果として何が起こるのかを、統計物理学や計算機シミュレーションなどの手法を用いて明らかにすること、それが我々の研究の目的です。より具体的には、原子・分子やスピンといった系の構成要素が互いに相反する要求をしあう、ランダム系やフラストレーション系を主な研究対象としています。
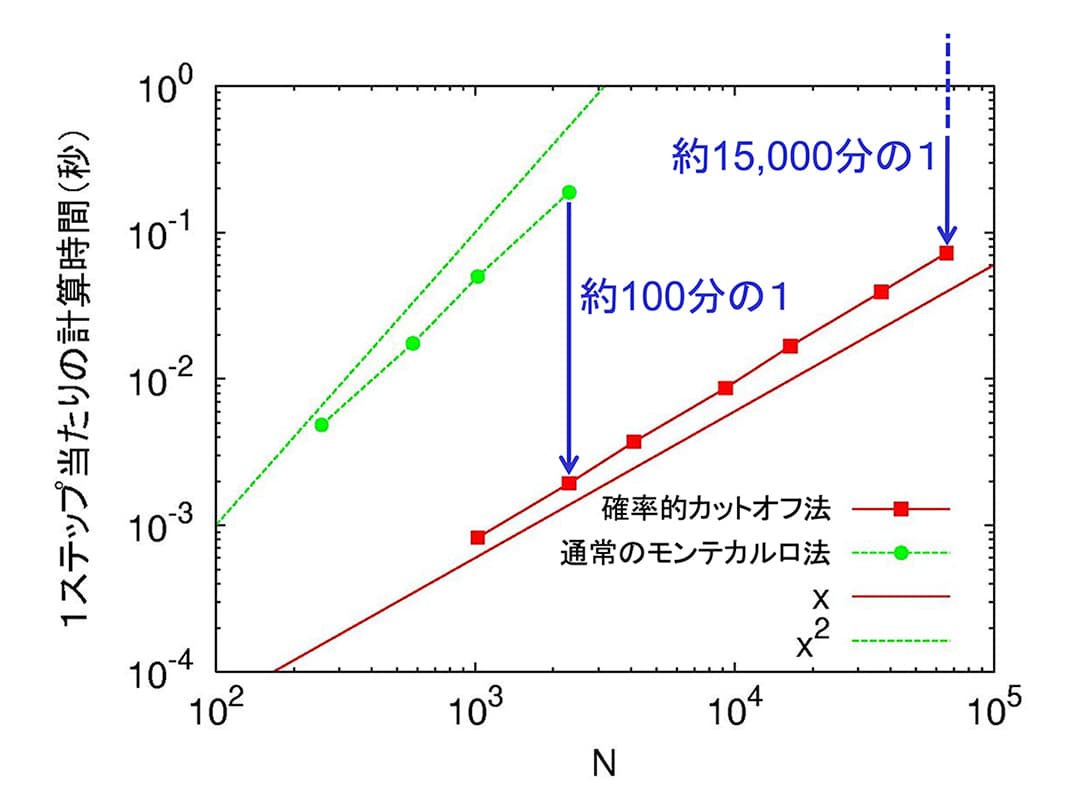
また、計算機シミュレーションのための、効率的な数値計算法の開発なども行っています。
ランダム系やフラストレーション系を、統計物理学や計算機シミュレーションなどの手法を用いて研究しています。また、ランダム系や長距離相互作用系において有効なシミュレーション手法の開発も行っています。ここでは、我々が開発したシミュレーション手法である、確率的カットオフ法について紹介します。
確率的カットオフ法は、長距離相互作用系において有効な手法で、モンテカルロ法として一切の近似をすることなく、長距離相互作用の計算時間を大幅に削減することができます。強磁性薄膜に対して確率的カットオフ法を適用した結果が図１で、長距離相互作用である磁気双極子相互作用の効果により、渦状の磁気構造が実現しています。また、計算時間のサイズ依存性を示したのが図２で、スピン数が2562=65,536の場合だと、通常のモンテカルロ法と比較して、計算時間が約15,000分の1となっています。
図1：強磁性薄膜の磁気構造
図2：計算時間のサイズ依存性
